Vector
선형 대수학의 가장 중요한 기본 요소 중 하나인 벡터이다.
n차원 <= 벡터 n가지이며, 아래와 같이 표현할 수 있다

위 사진에서는 X의 열 행렬 안의 실제 수들의 집합을 벡터값이라고 볼 수 있다
혹은 X transpose에서도 마찬가지로 내부의 수 집합을 벡터값이라 볼 수 있다

예시를 들어 위와 같은 벡터의 값은 X1, X2, X3의 방향으로 각각 이동한 [1, 3, 2]의 값을 가지고 있는 벡터라고 볼 수 있다
Scalar Multiplication
Scalar >> 방향이 존재하지 않는 온전한 값이다 정수, 실수 등이 이에 해당한다
벡터와 Scalar의 곱셈이다. 쉽게말해 방향별로 이동한 값에 각각 Scalar값을 곱해준다


Vector Addition
Vector값들의 덧셈이다
방법은 생각보다 간단하다
같은 행(또는 열)위치에 있는 요소끼리 더해주면 된다


Length of a Vector
벡터의 길이를 나타내는 방법이다
여기서 우리는 굉장히 친숙한 방법을 통해 길이를 구할 수 있다
바로 피타고라스의 정리로 유명한 공식인 (a^2 + b^2 = c^2)을 사용한다
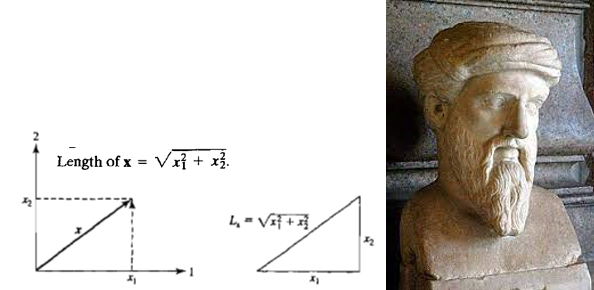
Angle
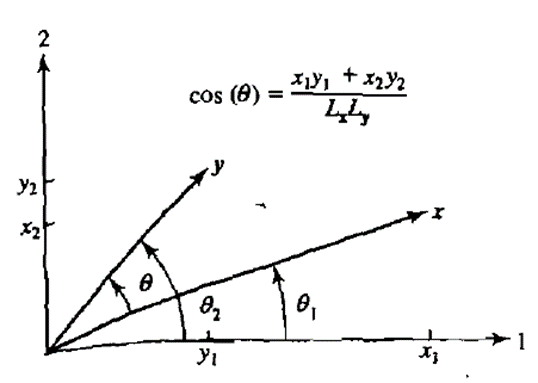
벡터의 각도는 주로 cosθ로 나타내어지며 이를 구하는 방식은 아래와 같다
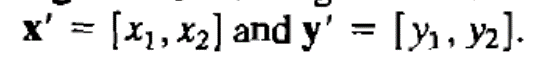

Orthogonal
우리말로 직교 라고 불리는 이 단어는 cosθ가 0이 되는 값으로 데이터적 측면에서는 관련도가 없는 정보로 분류된다
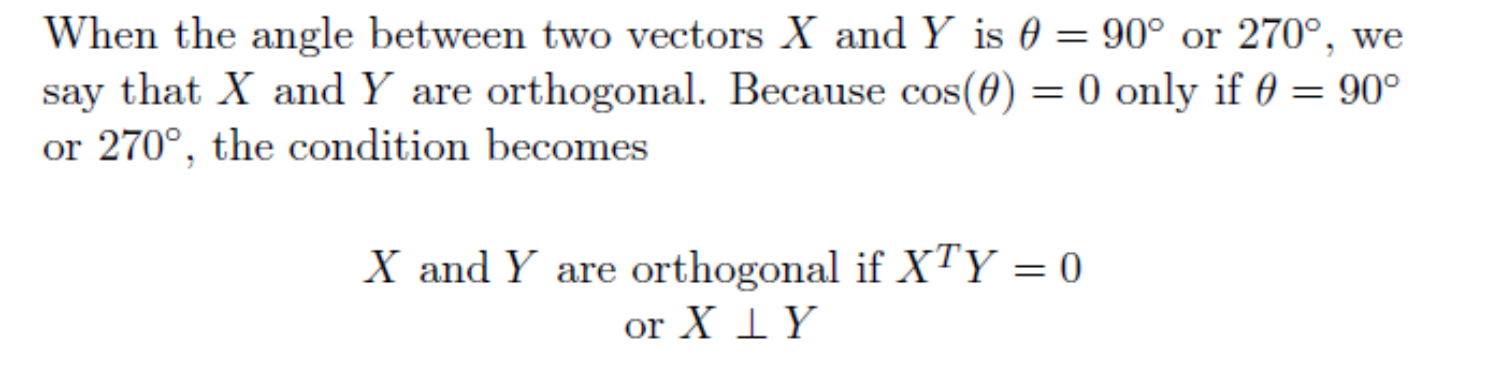
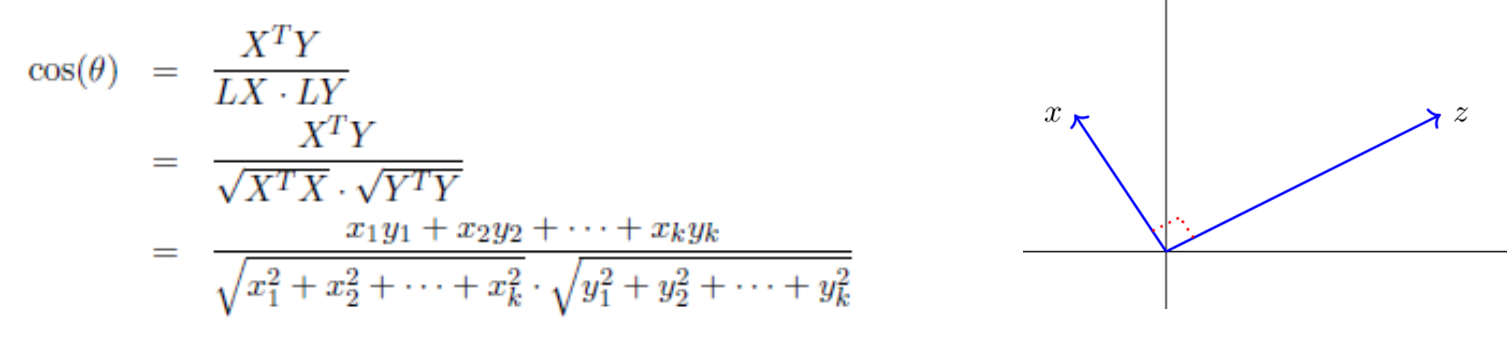
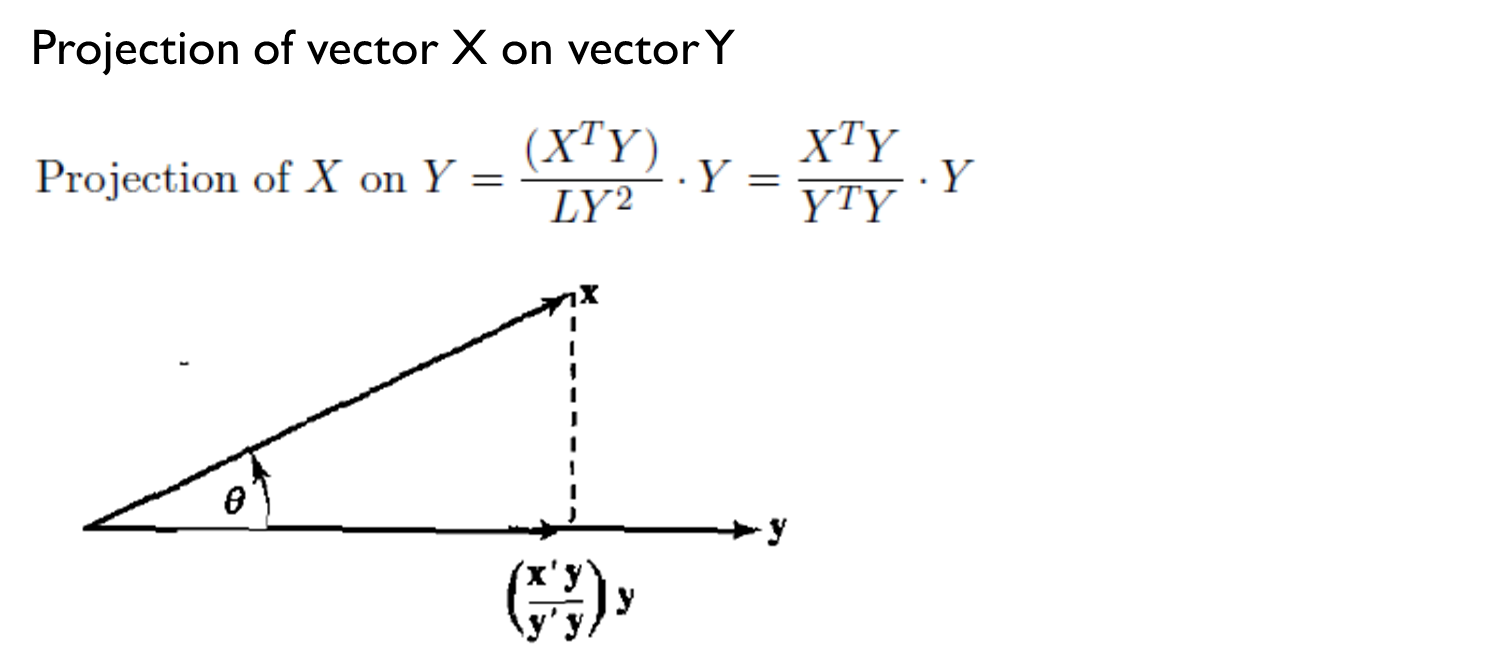
Projection
투사라는 뜻을 가지고 있는 단어로 한 벡터를 다른 벡터에 수직으로 내리는 것
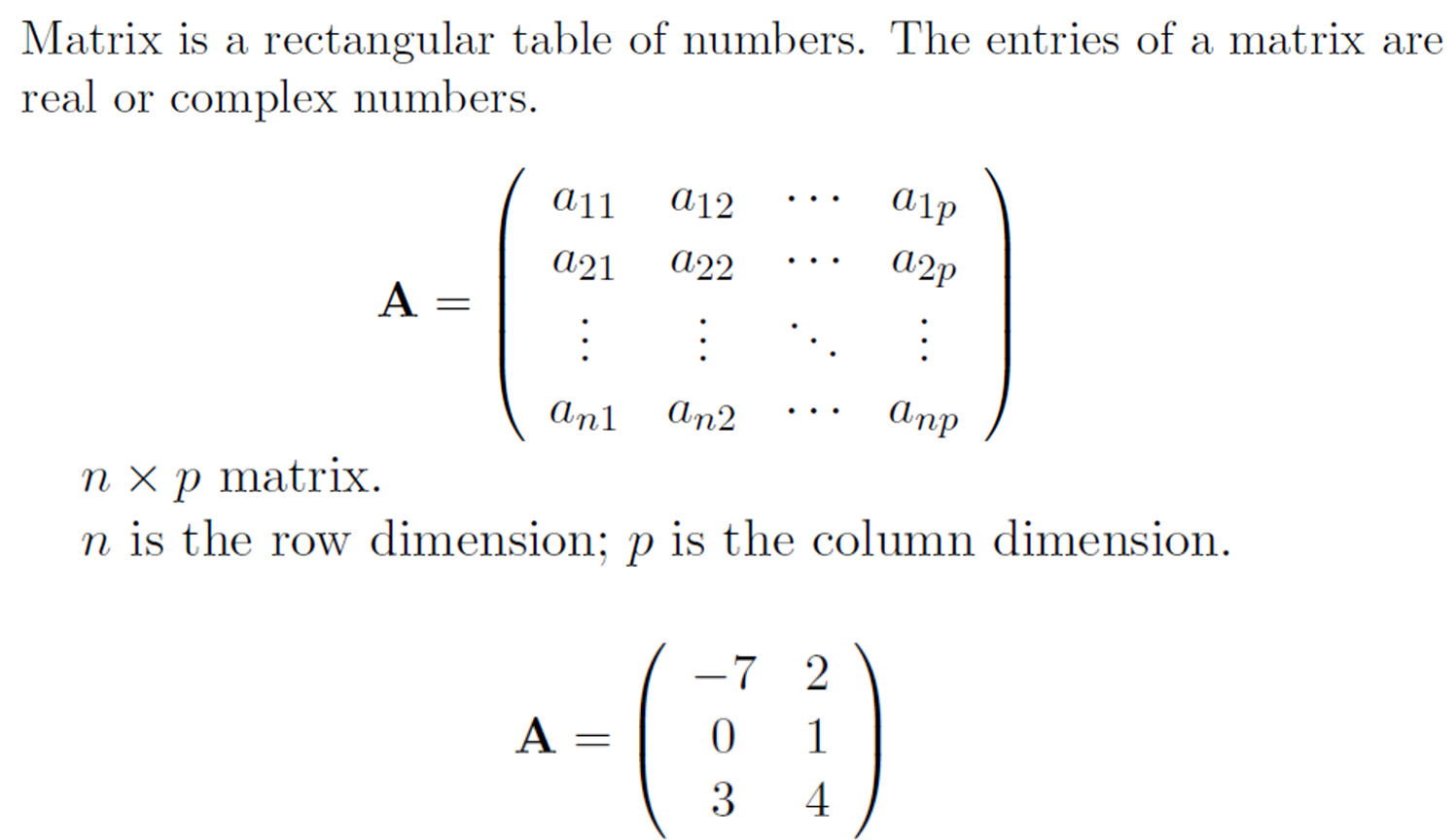
Matrix
매트릭스는 사각형으로 이루어신 수의 집합이다. 주로 nXp의 형태로 이루어져 있으며 실재하는 수들로 이루어져있다
Transpose
전치행렬을 뜻하며 x축과 y축을 바꾸어둔 듯한 모습을 하고 있다
주로 \ 방향으로 뒤집었다고 설명할 수 있다
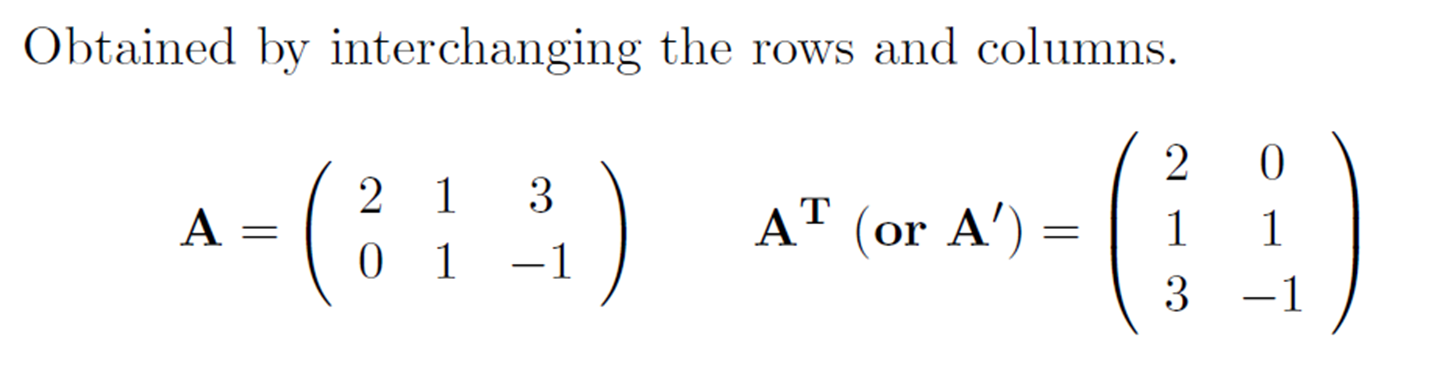
Square Matrix / Symmetric Matrix
행렬이 정사각형일 때 전치행렬과 같은 형태를 띄고 있다면 대칭 이라고 말할 수 있다
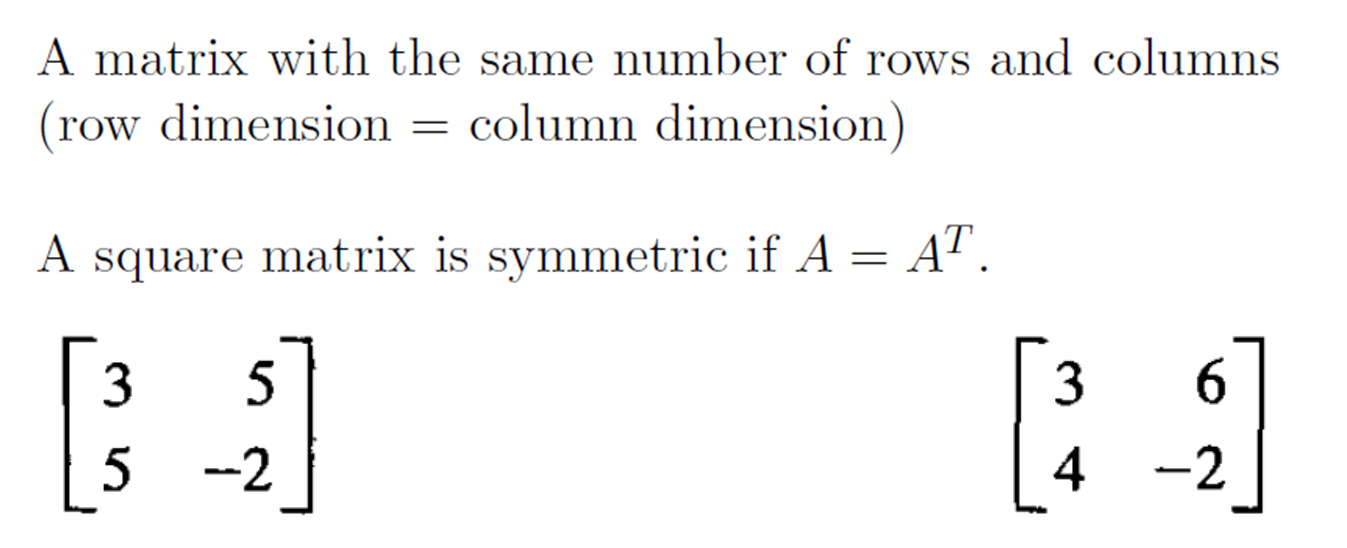
Matrix Addition
행렬끼리의 덧셈을 같은 위치에 있는 수 끼리만 더하면 된다
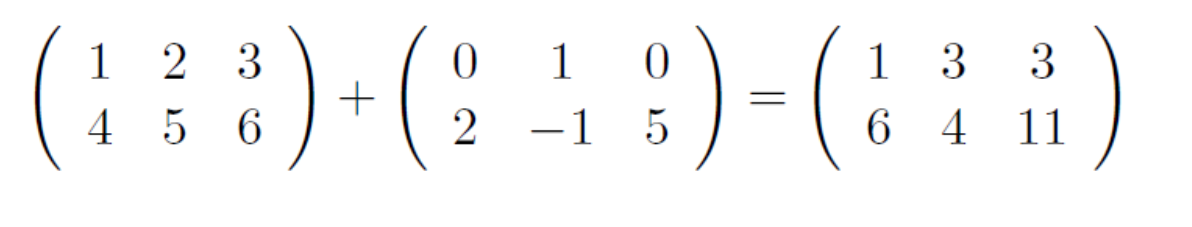
Scalar Multiplication
스칼라값과 행렬을 곱하면 모든 행렬의 요소에 스칼라값이 곱해진다
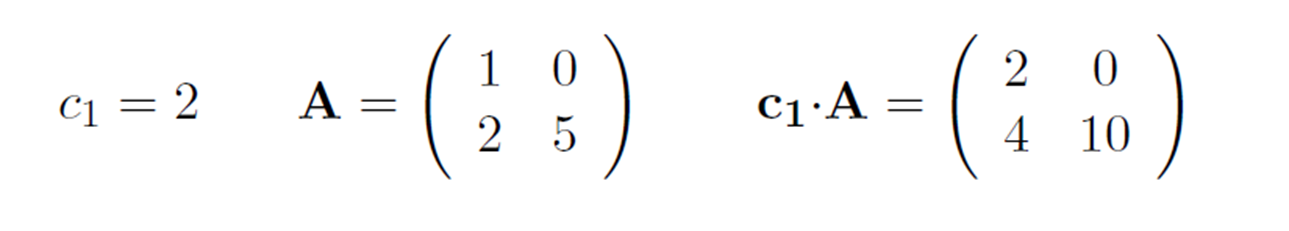
Matrix Multiplication
행렬끼리의 곱셈을 나타낸 그림이다
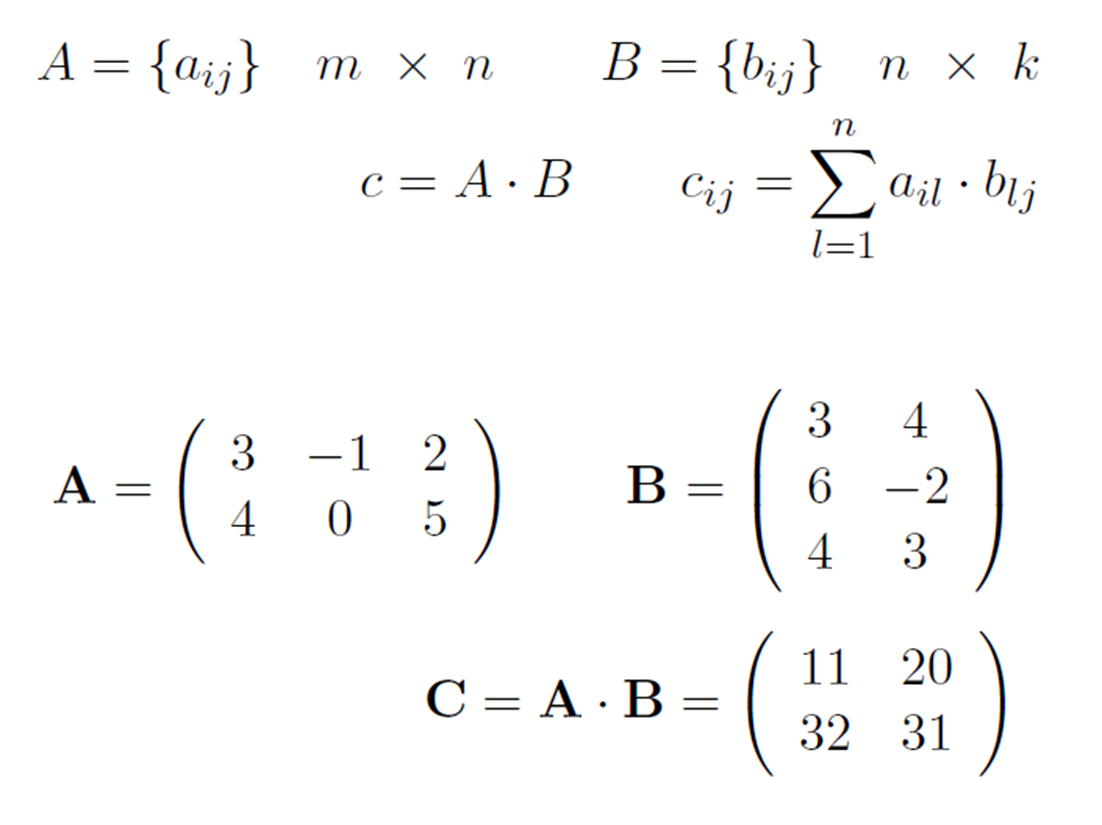
Determinant
정사각 형태이어야 한다
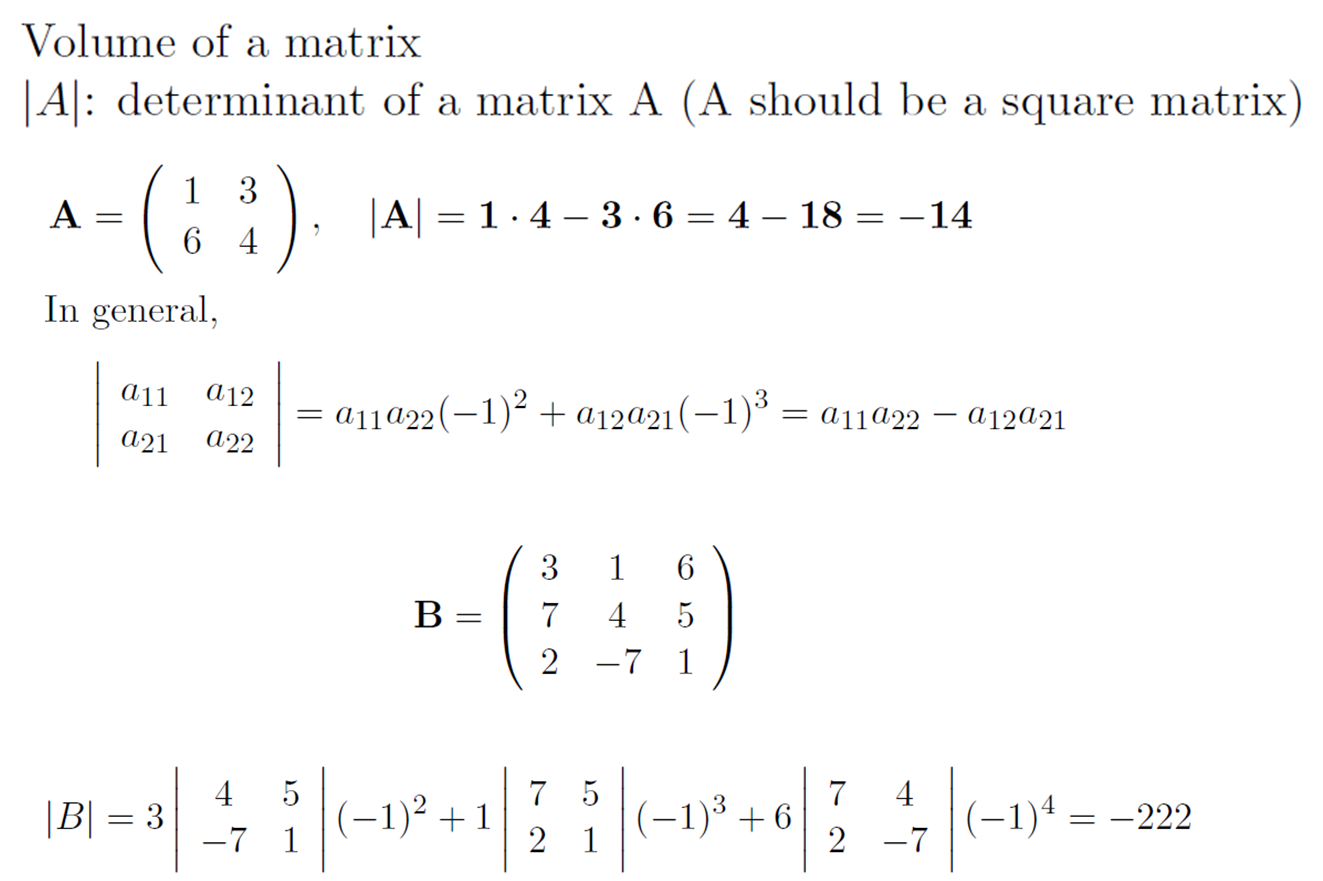
Matrix Inverse
역행렬이다

Trace of a Matrix
determinant에서 \ 방향에 있는 모든 값을 합한 것

'개발 외 공부 저장소 > 생산운영관리' 카테고리의 다른 글
| [프로세스 마이닝] 궤도에서 이탈하는 프로세스, 해결하는 방법은? (0) | 2022.10.06 |
|---|---|
| [생산운영관리] 생산운영이란 무엇일까 (0) | 2022.09.08 |